Значение использования индивидуального способа для воспитания младших школьников

Вова был под шифром 3, 16, 3, 1;

Анна – 1, 15, 15, 1; Нина – 15, 10, 15, 1.

От шифров ребят, которых звали Рома и Дима, остались лишь такие записи:

1 и 5. Помоги ребятам восстановить шифры этих мальчуганов.

IV. Предлагая упражнения на становление проективной подструктуры

мышления, имеем в виду знания ориентироваться в пространстве (на плоскости), чертить схемы к условию задачи, планировать.

1. Если на планете температура воздуха годично возрастает на 7 градусов, какая температура будет через 7 лет?

2. Сегодня мать старше сына в три раза (9 и 27 лет). Во сколько раз она будет старше его через 9 лет?

3. Выбери сам размеры школьного участка и начерти, как бы ты его спланировал, изображая 10 м отрезком в 1 см.

4 (М). Объедини точки отрезками так, дабы получилось 12 равносторонних треугольников с вершинами в этих точках.

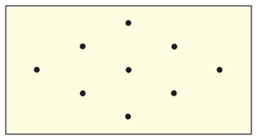
5 (М). Саша сказал брату: «Я начертил треугольник, поделил его одним отрезком на 2 части, вырезал их и составил прямоугольник. Додумайся, какого вида треугольник я начертил». Брат подумал и сказал: «Эта задача имеет два решения». Обнаружь их.

V. В топологической подструктуре развиваем знания определять объекты внутри и вне определенного пространства; ступенчато и безостановочно вычерчивать силуэт цифр, фигур, других объектов; разумно и доказательно обосновывать принятые решения, приходя к умозаключениям через рассуждения поэтапно, без обрывов в цепочке умственных реформирований.

1. Двигаясь по числовой прямой, докажи, что 8 + 7 = 15.

2. Назови все числа от 876 546 до 876 555.

3. Покажи линией, не отрывая руки, путь машины. Маршрут: 830, 700,

450, 780, 300. Линия при этом не должна пересекать себя.

800 – 350.860 – 30

720 + 50

1000 – 300.280 + 20

4. Подумай, как, не разрезая веревки и не снимая с нее других колец, снять только одно кольцо 3.

5. Объедини числа от 300 до 251.

Умение индивидуальных доминантных подструктур мышления учеников может оказать значительную подмога и при организации на уроке групповой работы. Традиционно группы составляются произвольно либо в соответствии с логическими соображениями учителя. Впрочем если совместно объединяются дети с разными доминантными подструктурами, то сплоченной работы, единомыслия ждать от них сложно. Такие группы уместно создавать в тех обстановках, когда дети обязаны выработать различные точки зрения, различные методы, различные решения. Помогает такая форма организации и тогда, когда мы хотим, дабы сверстники помогли своему товарищу принять другой

взор, позицию, другое решение.

Собрав в группу детей с идентичной подструктурой мышления, дозволено быть уверенным, что они легко и стремительно осознают друг друга и их совместная работа окажется производительной. Следственно при дифференциации детей для групповой работы нужно рассматривать их индивидуальные особенности и, в зависимости от дидактической цели, создавать группы с различными либо одной доминантной подструктурой мышления.

В индивидуальной работе с учениками умение доминантной подструктуры мышления всякого исключительно значимо, если появилась надобность вывести ученика из затруднения. Для этого с триумфом дозволено применять целевую подсказку. Скажем, при решении задач «топологу» отличнее предложить детально проанализировать связи всех элементов задачи (что из чего следует), составить логическую цепочку последовательности действий.

«Проективисту» легче будет решить задачу, если он сделает рисунок либо чертеж. «Порядковцу» следует напомнить, что существуют определенные правила при решении задач. «Метристу» надобно отчетливо определиться, что обозначает всякое число, и сделать ударение на количественных отношениях в задаче, а ребенку с ясно выраженной композиционной подструктурой будет легче совладать с заданием, если он определит, что есть часть, а что целое, и отчетливо поймет, что следует обнаружить по условию и вопросу задачи.

В качестве примера разглядим некоторые виды упражнений и вопросы, которые дозволено сформулировать, помогая ученику думать и рассуждать в «родной» подструктуре мышления при постижении темы «Сложение и вычитание в пределах 100».

Задача. На дорогу до спортивной школы требуется 15 минут на метро, после этого 20 минут на автобусе и 5 минут пешком. Сколько времени надобно на дорогу до спортивной школы?

1. Композиционная подструктура.

В этом случае подсказки основываются на представлениях целого и части.

– Если дорога от дома до спортивной школы – это целое, то какие части составляют дорогу от дома до школы? Часть – на метро, часть – на автобусе, часть – пешком.

– Обнаружь целое, состоящее из общности частей. Каким действием ты сделаешь это?

– Взамен частей произведи действия с величинами.

Это интересно:

Анализ деятельности Министерства образования и науки Челябинской области на примере управления дошкольного образования
Управление дошкольного образования является структурным подразделением министерства, обеспечивающим осуществление федеральной (в части, отнесенной к компетенции субъекта РФ) и региональной политики в сфере дошкольного образования. В своей деятельности специалисты управления руководствуются Конститу ...

Коррекционная работа по формированию первоначальных представлений о себе
Можно предположить, что коррекционная работа по формированию у умственно отсталого ребенка представлений о себе, развитие форм общения со взрослыми и детьми будут способствовать возникновению у него потребности к установлению определенных социальных отношений со своими сверстниками. Прежде всего мо ...

Ступени формирования орфографического навыка
Процесс формирования орфографического навыка проходит несколько ступеней. Первая ступень - учебная ситуация, которая порождает потребность проверить орфограмму. Ученик ставит перед собой цель, осознает задачу. Вторая ступень - поиск способа решения орфографической задачи: опора на знания, на правил ...