Значение использования индивидуального способа для воспитания младших школьников

Опираясь на порядковую подструктуру мышления, ребенок вычленяет свойства, устанавливает и систематизирует отношения по различным основаниям: по размеру (огромнее-поменьше, длиннее-короче), расстоянию (ближе-дальше, ниже-выше), форме (круглый, прямоугольный), расположению в пространстве (наверху-внизу, справа-слева, впереди-сзади, параллельно, перпендикулярно), временным представлениям (вначале-потом, до-позже, прежде-позднее) и т.д. Ученики с данной главенствующей подструктурой выбирают всё сопоставлять и оценивать в всеобщем добротном виде.

Действуют эти дети разумно, ступенчато, по порядку. Работа по алгорифму для них – любимое занятие.

Метрическая подструктура дозволяет вычленять в объектах и их компонентах количественные величины и отношения (размеры, углы, расстояния, протяженность, удаленность) в определенных числовых значениях. Эта подструктура акцентирует мышление ребенка на тех реформированиях, которые разрешают считать и находить числовые колляции объектов. Стержневой вопрос для них – «сколько?»: какова величина, длина, площадь, расстояние. С подмогой композиционной (алгебраической) подструктуры дети осуществляют прямые и обратные операции по реформированию объектов, исполняют операции в всякий последовательности. Дети с данной доминантой непрерывно тяготятся к всевозможным комбинациям и манипуляциям, вычленению частей и сбору их в цельное целое, к сокращению и замене нескольких реформирований одним. Такие дети не хотят и с большим трудом принуждают себя детально прослеживать, записывать, пояснять все шаги решения либо обосновывать личные действия. Думают и действуют они дюже стремительно, но при этом зачастую заблуждаются.

Данная модель, при условии ее принятия педагогом, открывает громадные вероятности для осуществления индивидуального метода к обучению учеников, потому что базируется на научно-психологическом видении индивидуальных отличий и особенностей мышления младших школьников.

Проиллюстрируем примером, как по-разному дети понимают одно и тоже, казалось бы, примитивное задание:

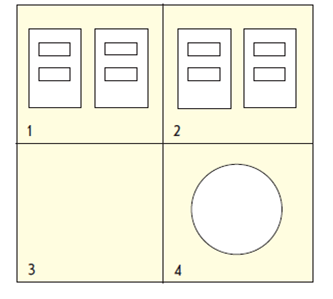
Расскажите, что вы видите на рисунке.

Результаты детей дозволено поделить на несколько групп в зависимости от главенствующей в мышлении ребенка подструктуры:

1. – в первом квадрате – двери либо окна; во втором квадрате – коробочки;

в третьем квадрате – пустое пространство, небосвод без облаков; рисунок

в четвертом квадрате схож на нашу Землю, когда на нее глядят с дальнего расстояния.

– Рисунок схож на радио, на кнопки в машине. – Крупной квадрат – как капот трактора без одной фары.

– Рисунок схож на окно, которое давным-давно не мыли.

Эти результаты свидетельствуют о доминировании у школьников проективной подструктуры, потому что дети устанавливают сходство (соответствие) между объектом и его моделями, разными изображениями.

2. В случае доминирования композиционной (алгебраической) подструктуры мышления результат может быть, скажем, таким:

– На рисунке не хватает одной части (она не дорисована).

Ясно, что эти дети раньше каждого вычленили компоненты, части рисунка и нашли, что одна из них пустая.

3. Результаты детей с главенствующей топологической подструктурой:

– Внутри рисунка – квадраты, в них – кружок и прямоугольники, а в них – еще прямоугольники.

– В квадрате – пустая клетка, рядом – замкнутый кружок, а выше идут еще геометрические фигуры.

Тут очевидно прослеживается доминирование представлений «внутри», «рядом», «совместно», «включение».

4. Школьники с порядковой доминантой предполагают, что на рисунке:

– Изображены геометрические фигуры – круг, квадраты и прямоугольники.

– Один крупный квадрат, маленькие квадраты, в нижнем правом квадрате – круг, в верхних левом и правом квадратах – крупные и маленькие прямоугольники.

Результаты свидетельствуют об акценте на форме и соотношениях фигур («крупный-небольшой»), их расположении.

5. У детей с развитой метрической подструктурой результаты могут быть такими:

– 21 четырехугольник, 1 круг.

– Три заполненных и один пустой квадрат.

– 12 прямоугольников внутри 2‑х квадратов.

Выходит, отличия в мышлении учеников очевидны, следственно мы обязаны не столько оценивать, сколько понимать и принимать логику их рассуждений, оставляя за детьми право на индивидуальность.

Как водится, младший школьник мыслит, опираясь на образы и представления, в своей «родной», доминантной подструктуре. Задача педагога – выявить ее и сориентироваться в индивидуальных особенностях мышления всего. Приведем пример такой диагностики.

Задание. Выдели «ненужный» предмет из 5 предложенных. Объясни свой выбор.

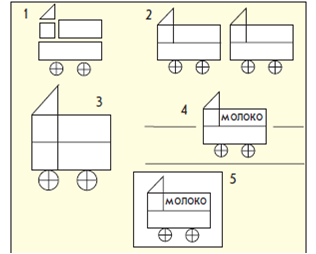
Допустимые формы проведения диагностики: а) задание предлагается индивидуально, на карточках; б) результаты озвучиваются самим учителем, а дети выбирают один из предложенных вариантов; в) учащиеся независимо исполняют задание и поясняют свой выбор в группе (в классе).

Это интересно:

Программа повышения квалификации "Университет и общество: социальные функции и ответственность" в УрФУ
Фонд «Новая Евразия» в сотрудничестве с Центром повышения квалификации в области международного сотрудничества Уральского Федерального университета имени Первого Президента России Б.Н.Ельцина, Посольством Италии в Москве и Болонским университетом реализуют Программу повышения квалификации для сотру ...

Психолого-педагогический аспект в обучений английскому языку на среднем этапе
Психолого-педагогический аспект проблемы обучения иностранному языку в начальной и средней школе. Согласно многим периодизациям психического развития личности, подростковый возраст определяется периодом жизни человека от 11–12 до 14–15 лет – периодом между детством и юностью. Это один из наиболее к ...

Средства и методы воспитания культуры поведения детей старшего дошкольного возраста
Нравственное воспитание определяется с помощью определенных средств, среди которых необходимо указать: художественные средства; природу; собственную деятельность детей; общение; окружающую обстановку. 1. Группа художественных средств: художественная литература, изобразительное искусство, музыка, ки ...